Recent advancements in generalization bounds have led to the development of tight information theoretic and data-dependent measures. Although generalization bounds reduce bias in estimates, they often suffer from tractability during empirical evaluation. The lack of a uniform criterion for estimation of Mutual Information (MI) and selection of divergence measures in conventional bounds hinders utility to sparse distributions. To that end, we revisit generalization through the lens of variational bounds. We identify hindrances based on bias, variance and learning dynamics which prevent accurate approximations of data distributions. Our empirical evaluation carried out on large-scale unsupervised visual recognition tasks highlights the necessity for variational bounds as generalization objectives for learning complex data distributions. Approximated estimates demonstrate low variance and improved convergence in comparison to conventional generalization bounds. Lastly, based on observed hindrances, we propose a theoretical alternative which aims to improve learning and tightness of variational generalization bounds. The proposed approach is motivated by contraction theory and yields a lower bound on MI.

Why Generalization?

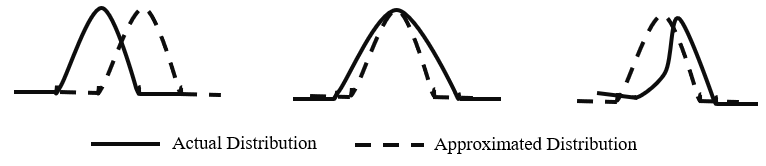
The work throws light on the behavior of tractable distributions with high dimensional random variables. Based on the empirical characteristics of these bounds, one can identify the hindrances faced in generalization of the leanring algorithm (see figure).

High Variance: Normalized upper and lower bounds aid in tractability of variational distributions when the data to be learned is long-tailed. However, these bounds demonstrate high variance as a result of large MI estimates. A suitable alternative to normalized bounds is to adopt the framework of structured bounds. These bounds leverage the structure of the problem and yield a known conditional distribution which is tractable as per the problem setting. Structured bounds are conveniently applicable to representation learning but do not necessarily scale to high-dimensional scenarios. Another alternative which provisions a conditional tractable distribution are reparameterization bounds. These bounds make use of an additional functional, known as the critic, which converts lower bounds on MI into upper bounds on KL divergence. The critic functional need not explicitly learn the mapping between $x$ and $y$. However, reparameterization is only made feasible if the conditional distribution is tractable.

High Bias: Unnormalized upper and lower bounds demonstrate high bias and hurt tractability of complex distributions. Primary reasons for instability in bounds is lack of a partition functional which normalizes MI estimates. Other works argue that requirement of a partition function presents high bias as a result of exponential distributions which may not be tractable. However, the work does not provide empirical evidence on their tractability which leaves the suitability of a normalization constant an open question. A suitable alternative to address biased estimates is the adoption of density ratios which train the critic functional using a divergence metric. The Jensen-Shanon Divergence (JSD) is one such scheme which yields a lower-biased estimate of optimal critic. While training critics is theoretically suitable, empirical evaluations demonstrate unstable convergence of exponential gradients.

A Failure to Learn: Biased and noisy estimates are the key hindrances in learning tractable distributions. To that end, various works aptly propose a continuum of multi-sample interpolation bounds which trade-off bias with variance. A simpler form of critic when applied to non-linear interpolation in InfoNCE samples yields a continuum of lower bounds on MI. The new bound can be manually tuned using $\gamma$ which trades off bias with variance. Nonlinear interpolation bounds proposed in conjunction with MI saturate at $\log \frac{K}{\gamma}$ with $K$ being the number of samples in the batch. Saturation of interpolation hurts the completeness of distribution and the bound fails to learn large MI estimates with increasing batch sizes.

Learning Variational Bounds

InfoNCE: The InfoNCE objective is based on multi-sample unnormalized bounds. These bounds formulate multi-sample MI $I(X_{1};Y)$ which is bounded by the optimal choice of critic $f(x,y)$. One such formulation is based on MINE which employs a Monte-Carlo estimate of the partition function $Z(y)$ expressed below. \begin{gather} m(y;x_{1:K}) = \frac{1}{K}\sum_{k=1}^{K}e^{f(x_{k},y)} \end{gather}

One can recover the InfoNCE bound ($I_{NCE}$) upon averaging over all $K$ replicates in the last term which yields 1. $I_{NCE}$ can then be expressed as a lower bound on MI.

\begin{gather} I(X;Y) \geq \mathbb{E}[\frac{1}{K}\sum_{k=1}^{K}\log\frac{e^{f(x_{k},y_{k})}}{\frac{1}{K}\sum_{j=1}^{K}e^{f(x_{k},y_{j})}}] \triangleq I_{NCE} \end{gather}

Nonlinear Interpolation: The multi-sample framework of MINE can be further extended using a simpler formulation. A nonlinear interpolation between MINE and $I_{NCE}$ bridges the gap between low-bias and high-variance estimates of MINE with high-bias and low-variance estimates of $I_{NCE}$.

While $I_{NCE}$ is upper bounded by $\log K$, $I_{IN}$ is upper bounded by $\log \frac{K}{\gamma}$. The control in bias-variance trade-off improves accuracy of estimates. However, the significance of $\gamma$ remains an open question in the case of higher-order divergence metrics and large value of MI in practical settings.

$\phi$-divergence: Generalized divergence metrics facilitate tighter bounds by utilizing $\alpha$-MI as the dependence measure. Various works present a tight bound which is based on random variables with cumulant-generation functions. If $X_{i}-Y_{i}$ has a cumulant generation function $\leq \psi_{i}(\lambda)$ over domain $[0,b_{i})$ where $0 \leq b_{i} \leq \infty$ and $\psi_{i}(\lambda)$ is convex and $i$ denotes the iterates of the variables $X$ and $Y$, one can define the expected cumulant-generation function $\bar{\psi_{i}}(\lambda)$ to obtain the bound.

\begin{gather} \bar{\psi}(\lambda) = \mathbb{E} [\psi_{i}(\lambda)],\; \lambda \in [0,\underset{i}{\min} b_{i}) \end{gather}

\begin{gather} \mathbb{E}[X_{i} - Y_{i}] \leq \bar{\psi}^{*-1}(I(X;Y)) \end{gather}

The bound generalizes previous works as it is applicable to long-tailed distributions and variables which may not necessarily obey the sub-Gaussianity assumption.

While the bound is generalizable to variables with no moment-generating functions, its tightness remains an open question. Previous works prove the tightness of bound using extreme value theory. The bound is tight for $n^{\frac{1}{\beta}}$ with $n$ being the number of data samples. However, tightness holds under the condition that $\beta$ is bounded such that $2 \leq \beta \leq \infty$. For large values of $\beta$, $n^{\frac{1}{\beta}}$ tends to diminish which renders the estimation of $I_{\alpha}(X;Y)$ intractable. Moreover, $\phi$-divergences are originally defined as power functions over $\beta$ while the bound makes use of an affine transformation. The alternate formulation may not hold in the more generalized-case. This poses a hindrance for $\alpha$-MI bounds to be used as substitutes to pre-existing methods.

Generalization in Unsupervised Visual Recognition

Our experiments consist of unsupervised instance discrimination tasks which involve the recognition of images based on MI. The setup consists of three standard benchmarks; MNIST, FashionMNIST and CIFAR10, and two large-scale datasets; EMNIST (Letters) and CIFAR100. In order to study the effect of deep architectures we employ ResNET-18 and ResNet-34 modules. The comparison consists of 4 different MI objectives with InfoNCE (as expressed in $I_{NCE}$) and Donsker-Vardhan (DV) loss as conventional objectives and Jensen-Shannon Divergence (JSD) and Reverse KL (RKL) as $\phi$-divergence measures. Each objective maximizes similarity between logits and feature representations. The fully-supervised Cross-Entropy (CE) is additionally considered as a baseline. Objectives on the standard benchmarks are trained and evaluated for 200 epochs while large-scale datasets make use of 600 epochs.

To better understand convergence and tightness of variational bounds, one can gain visual insights into their behavior during learning. Plots below present comparison of generalization error during training for all objectives on standard and large-scale benchmarks utilizing the ResNet-18 and ResNet-34 architectures. Insights obtained validate our claims on generalization. Unsupervised variational objectives demonstrate improved generalization as a result of minimimum validation error in comparison to the fully-supervised CE objective. Moreover, consistency of these objectives across all datasets validates stability in convergence. Out of unsupervised objectives, JSD and RKL demonstrate equivalent errors with JSD slightly outperforming the latter. Suitability of JSD on standard and large-scale datasets further validates its robustness to large sample sizes. This is not found consistent in InfoNCE which depicts slightly higher errors and delayed convergence on EMNIST and CIFAR100 datasets.

Final Notes

Generalization bounds present significant promise for yielding accurate learning algorithms. However, these bounds are often held intractable during empirical evaluation. To this end, we have revisited the generalization setup from the perspective of variational bounds of MI. Firstly, we identified failure modes which hinder a bound to learn data as a result of bias and variance in estimates. We then carry out empirical evaluations of variational bounds under the generalization setup in order to identify potential generalization candidates. Our study highlights the suitability of $\phi$-divergences in $\alpha$-MI as suitable alternatives for generalization. Specifically, JSD and RKL demonstrate improved generalization on datasets with small and large sample sizes. Their performance is additionally found consistent on deeper architectures.